速度ポテンシャルの導入
波動方程式をポテンシャルを用いた形にする
さて、ようやく下記の波動方程式が導出されたわけですが、この式をどう解いたらいいのでしょうか。
$$ \displaystyle\frac{\partial ^2 p}{\partial t^2} = c^2 \nabla ^2 p \tag{9} $$
方程式ですから、\(p\)について解けば音圧が求められるということだとは思います。しかし、この\(p\)というのは3次元のベクトル関数(つまり、位置によって方向や大きさの変わる関数)なので、上記の波動方程式はベクトル方程式ということになります。3次元のベクトル方程式はそのままでが解けないので、スカラーポテンシャルという考え方を用いることで、波動方程式が単なる微分方程式になるので容易に解けるようになります。
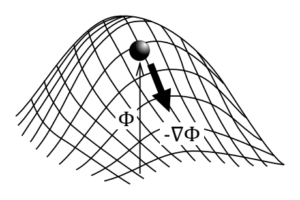
そもそもベクトル関数は、方向ベクトルと大きさとからなる関数です。山がよく例に挙げられますが、山から転げ落ちるボールの速度は山が高い方が速くなるでしょうし、稜線の傾きが急な方が速くなることになります。
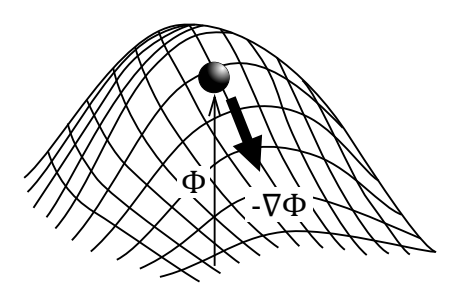
つまり、速度ベクトルは、山の稜線の傾き方向\( \nabla\)と山の高さ\(\phi\)とから定義できます。この例で、山の高さそのものは方向性を持たないスカラーであり、ボールは、山の高さに応じた速度で山の稜線の下る方向に沿って転がります。この例えでいう、山の高さ\(\phi\)に相当するものがスカラーポテンシャルです。
このスカラーポテンシャルは、傾き方向で微分することでベクトルとなるスカラー関数として定義されます。ちなみに、スカラーポテンシャルが大きいほどベクトルは大きくなりますが、その方向はポテンシャルが小さくなる方向に向くため、符号はマイナスとなります。ちょうど、山の高さの高い方から低い方へボールが落ちるイメージです。
さて、本題に戻って、ベクトルである速度\( u_x\),\( u_y\),\( u_z\)を速度ポテンシャル\( \phi\)として定義しますと、下記のようになります。
$$ u_x=-\displaystyle\frac{\partial \phi}{\partial x} \ u_y = -\displaystyle\frac{\partial \phi}{\partial y} \ u_z=-\displaystyle\frac{\partial \phi}{\partial z} $$
そして、例えば、上記の速度ポテンシャルを用いた( u_x)の式を、運動方程式に代入しますと、音圧\(p\)は下記のように表すことができます。
$$ \begin{align} \require{cancel} \displaystyle\frac{\partial u_x}{\partial t} &= -\displaystyle\frac{1}{\rho_0} \displaystyle\frac{\partial p}{\partial x} \\ -\displaystyle\frac{\partial ^\cancel{2} \phi}{\cancel{\partial x} \partial t} &= -\displaystyle\frac{1}{\rho_0} \displaystyle\frac{\cancel{\partial} p}{\cancel{\partial x}} \\ \unicode{x2234} p &= \rho_0 \dfrac{\partial \phi}{\partial t} \end{align} $$
これを、ベクトルの波動方程式(9)に代入しますと、下記のようになります。
$$ \begin{align} \require{cancel} \displaystyle\frac{\partial ^2 p}{\partial x^2} &= c^2 \nabla ^2 p \\ \cancel{\rho_0} \displaystyle\frac{\partial ^2}{\partial t^2} \displaystyle\frac{\cancel{\partial} \phi}{\cancel{\partial t}} &= c^2 \nabla ^2 \cancel{\rho_0} \displaystyle\frac{\cancel{\partial} \phi}{\cancel{\partial t}} \end{align}$$
$$ \unicode{x2234} \dfrac{\partial ^2 \phi}{\partial t^2} = c^2 \nabla ^2 \phi \tag{10} $$
このように、ベクトルである速度をスカラーポテンシャルである速度ポテンシャルで表現しても、波動方程式の形はそのままに、単純な微分方程式として解けるようになります。
波動方程式を極座標系に変換する
ところで、ポテンシャル表示した波動方程式(10)は、x,y,zの直交座標系の式になっています。音波がx,y,zのいずれかと平行な方向に入射する平面波であれば、この式を用いてもいいようです。しかし、一般的に、ある音源から放射される音波は、音源に近い位置ではあらゆる方向に広がっていく球面波となります。球面波はx,y,z方向に関わらず中心から放射状に伝播するので、極座標系で考えた方がいろいろ都合が良いということです。
直交座標系を極座標系に変換するために、まず、原点が音源である半径rの球を考えます。この場合、原点から球の表面上における任意の点までの距離は、\( r=\sqrt{x^2+y^2+z^2}\)と表すことができます。そして、距離(r)をx方向について方向微分すると、下記となります。
$$ \begin{align} \displaystyle\frac{\partial r}{\partial x} &= \displaystyle\frac{\partial}{\partial x} { (x^2+y^2+z^2)^{\frac{1}{2}} } \\ &= \displaystyle\frac{1}{2}(x^2+y^2+z^2)^{-\frac{1}{2}} \cdot 2x \\ &= x \cdot \displaystyle\frac{1}{\sqrt{x^2+y^2+z^2}} \\ &= \displaystyle\frac{x}{r} \end{align} $$
これを踏まえると、速度ポテンシャル( \phi)のx方向の方向微分は、
$$ \begin{align} \displaystyle\frac{\partial \phi}{\partial x} &= \displaystyle\frac{\partial \phi}{\partial r} \displaystyle\frac{\partial r}{\partial x} \\ &= \displaystyle\frac{x}{r} \displaystyle\frac{\partial \phi}{\partial r} \end{align} $$
となりますので、速度ポテンシャル( \phi)の二階微分は
$$ \begin{align} \displaystyle\frac{\partial ^2 \phi}{\partial x^2} &= \displaystyle\frac{\partial}{\partial x} \displaystyle\frac{\partial \phi}{\partial x} \\ &= \displaystyle\frac{\partial}{\partial x} \left( \displaystyle\frac{x}{r} \displaystyle\frac{\partial \phi}{\partial r} \right) \\ &= \displaystyle\left\{ \displaystyle\frac{\partial}{\partial x} \left( \displaystyle\frac{x}{r} \right) \displaystyle\right\} \displaystyle\frac{\partial \phi}{\partial r} + \displaystyle\frac{x}{r} \left( \displaystyle\frac{\partial}{\partial x} \displaystyle\frac{\partial \phi}{\partial r} \right) ^{※1} \\ &= \displaystyle\frac{1 \cdot r – x \frac{\partial r}{\partial x}}{r^2}^{※2} \displaystyle\frac{\partial \phi}{\partial r} + \displaystyle\frac{x}{r} \left( \displaystyle\frac{\partial}{\partial r} \displaystyle\frac{\partial r}{\partial x} \cdot \displaystyle\frac{\partial \phi}{\partial r} \right) \\ &= \displaystyle\frac{r-x\frac{x}{r}}{r^2}\displaystyle\frac{\partial \phi}{\partial r} + \displaystyle\frac{x^2}{r^2} \displaystyle\frac{\partial ^2 \phi}{\partial r^2} \\ &= \displaystyle\frac{r^2 – x^2}{r^3} \displaystyle\frac{\partial \phi}{\partial r} + \displaystyle\frac{x^2}{r^2} \displaystyle\frac{\partial ^2 \phi}{\partial r^2} \\ &= \displaystyle\frac{y^2+z^2}{r^3} \displaystyle\frac{\partial \phi}{\partial r} + \displaystyle\frac{x^2}{r^2} \displaystyle\frac{\partial ^2 \phi}{\partial r^2} \end{align} $$
となります。
※1は\( (f\cdot g)’=( f’ \cdot g +f \cdot g’)\)を使っています。
※2は\( (\frac{g}{f})’= \frac{g’\cdot f-g \cdot f’}{f^2}\)を使っています。
これをy方向とz方向についても求め、まとめると、
$$ \begin{align} \displaystyle\frac{\partial ^2 \phi}{\partial x^2} &= \displaystyle\frac{y^2+z^2}{r^3} \displaystyle\frac{\partial \phi}{\partial r} + \displaystyle\frac{x^2}{r^2} \displaystyle\frac{\partial ^2 \phi}{\partial r^2} \\ \displaystyle\frac{\partial ^2 \phi}{\partial y^2} &= \displaystyle\frac{z^2+x^2}{r^3} \displaystyle\frac{\partial \phi}{\partial r} + \displaystyle\frac{y^2}{r^2} \displaystyle\frac{\partial ^2 \phi}{\partial r^2} \\ \displaystyle\frac{\partial ^2 \phi}{\partial z^2} &= \displaystyle\frac{x^2+y^2}{r^3} \displaystyle\frac{\partial \phi}{\partial r} + \displaystyle\frac{z^2}{r^2} \displaystyle\frac{\partial ^2 \phi}{\partial r^2} \end{align} \tag{11} $$
となります。
これら式(11)を、ポテンシャル表示した波動方程式(10)に適用することで、極座標系の波動方程式を得ることができます。波動方程式における\( \nabla ^2 \phi\)の部分は、式(11)を足し合わせたものであるので、波動方程式(10)は下記のようになります。
$$ \begin{align} \displaystyle\frac{\partial ^2 \phi}{\partial t^2} &= c^2 \nabla ^2 \phi \\ &= c^2 \left( \displaystyle\frac{2(x^2+y^2+z^2)}{r^3} \displaystyle\frac{\partial \phi}{\partial r} + \displaystyle\frac{x^2+y^2+z^2}{r^2} \displaystyle\frac{\partial ^2 \phi}{\partial r^2} \right) \\ &= c^2 \left( \displaystyle\frac{2r^2}{r^3} \displaystyle\frac{\partial \phi}{\partial r} + \displaystyle\frac{r^2}{r^2} \displaystyle\frac{\partial^2 \phi}{\partial r^2} \right) \\ &= c^2 \left( \displaystyle\frac{2}{r} \displaystyle\frac{\partial \phi}{\partial r} + \displaystyle\frac{\partial ^2 \phi}{\partial r^2} \right) \\ &= c^2 \displaystyle\left\{ \displaystyle\frac{1}{r} \left(2\displaystyle\frac{\partial \phi}{\partial r} + r \displaystyle\frac{\partial ^2 \phi}{\partial r^2} \right) \displaystyle\right\} \\ &= c^2 \displaystyle\left\{ \displaystyle\frac{1}{r} \left( \displaystyle\frac{\partial \phi}{\partial r} + (1 \cdot \displaystyle\frac{\partial \phi }{\partial r} + r \displaystyle\frac{\partial^2 \phi}{\partial r^2}) \right) \displaystyle\right\} \\ &= c^2 \displaystyle\left\{ \displaystyle\frac{1}{r} \left( \displaystyle\frac{\partial \phi}{\partial r} + \displaystyle\frac{\partial}{\partial r} (r \displaystyle\frac{\partial \phi}{\partial r})^{※3} \right) \displaystyle\right\} \\ &= c^2 \displaystyle\left\{ \displaystyle\frac{1}{r} \displaystyle\frac{\partial}{\partial r} \left( \phi + r\displaystyle\frac{\partial \phi}{\partial r} \right) \displaystyle\right\} \\ &= c^2 \displaystyle\frac{1}{r} \displaystyle\frac{\partial ^2 (r \phi)}{\partial r^2} \\ r\displaystyle\frac{\partial ^2 \phi}{\partial t^2} &= c^2 \displaystyle\frac{\partial ^2 (r \phi)^{※4}}{\partial r^2} \end{align} $$
$$ \begin{align} \unicode{x2234} \displaystyle\frac{\partial ^2 (r \phi)^{※5}}{\partial t^2} &= c^2 \displaystyle\frac{\partial ^2 (r \phi)}{\partial r^2} \end{align} \tag{12}$$
この式(12)は球面波における波動方程式を表します。
※3※4は\( (f\cdot g)’=( f’ \cdot g +f \cdot g’)\)を使っています。
※5は、\(r\)と\(t\)が独立した変数であるため、\(t\)の偏微分においては\(r\)を定数扱いにできることを利用しています。
波動方程式を複素数形式で表す
ところで、上記のような微分方程式を解くとき、一般解のわかっている方程式の形であれば解くのが容易になります。そこで、上記方程式を特定の形に変形することを試みます。
準備段階として、速度ポテンシャル\( \phi\)はどのようなものであるかを改めて考えてみます。\( \phi\)は空気を粒子の集まりと考えたときの、空気の粒の速度をポテンシャルとして表したものでした。空気の粒は、粗密波を構成する要素として前後に正弦波の形で動いています。つまり、時間( t)によって位置が変動する関数であると考えられます。その関数の形は、振幅Aを1とすると下記のようになると考えられます。
$$ \phi = sin ( 2 \pi ft) = sin ( \omega t )$$
ここで少し脱線しますが、上記の式には\(sin\)という三角関数が出てきます。三角関数はそのまま微積分するよりも、複素数の形に変換した方が都合がよいのです。(sin)関数を複素数で表すと、以下のような簡単な指数の形になります。
$$ \phi = e^{j \omega t} \tag{13}$$
なぜ都合がよいかというと、この形は\(t\)で微積分すると、下記のように\( j \omega\)の掛け算・割り算となるため、計算が非常に簡単になるという特徴があります。
$$ \begin{align} 1階微分 \quad &\displaystyle\frac{d}{dt} e^{j \omega t} = j \omega e^{j \omega t} \\ 2階微分 \quad &\displaystyle\frac{d^2}{dt^2} e^{j \omega t} = j \omega j \omega e^{j \omega t} = – \omega ^2 e^{j \omega t} \\ 積分 \quad &\int e^{j \omega t} dt = \displaystyle\frac{1}{j \omega} e^{j \omega t} \\ 重積分 \quad &\iint e^{j \omega t} dtdt = \displaystyle\frac{1}{j \omega} \displaystyle\frac{1}{j \omega} e^{j \omega t} = -\displaystyle\frac{1}{\omega ^2} e^{j \omega t} \end{align}$$
なぜ正弦波の式を(13)のように表すことができるのか説明してみます。
一般的に、正弦波\( y = sin ( \omega t )\)の時刻\( t\)における位置(座標)は、時間軸座標では右図のようになり、極座標では左図のようになります。
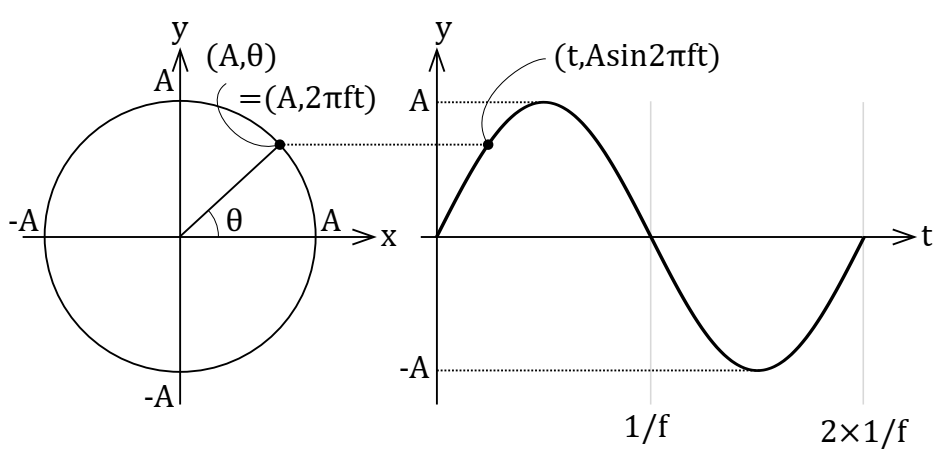
このように、極座標にすると周期的に表れる同形の波形を、ひとつの円で表現することができ、任意の時間における位置(座標)は\( (1, \theta) = (1, \omega t)\)と表すことができます。
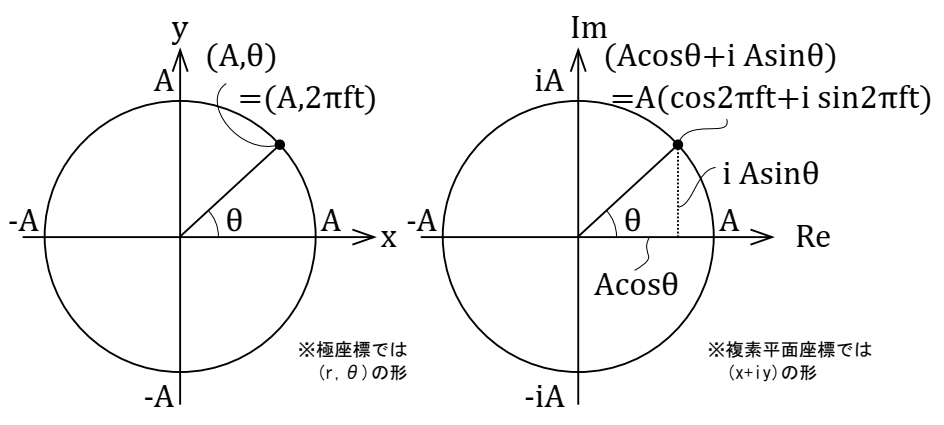
さらに、極座標を、複素平面座標で表すと、下図における右図のようになり、任意の時間における位置(座標)は\( cos ( \theta ) + j sin ( \theta) = cos (\omega t) + j sin ( \omega t)\)と表すことができます。
※図中の虚数単位の\(i\)は、音響の式の中では\(j\)に置き換えています。電流と混同しやすいためです。
一方で、三角関数はテイラー展開すると、下記のようになります。
$$ \require{color} \textcolor{red} { cos \theta = 1 – \displaystyle\frac{\theta^2}{2!} + \displaystyle\frac{\theta^4}{4!} – \displaystyle\frac{\theta^6}{6!} + \displaystyle\frac{\theta^8}{8!} \cdots }$$
$$ \require{color} \textcolor{blue} { sin \theta = \theta – \displaystyle\frac{\theta^3}{3!} + \displaystyle\frac{\theta^5}{5!} – \displaystyle\frac{\theta^7}{7!} + \displaystyle\frac{\theta^9}{9!} \cdots }$$
ということは、複素平面座標における任意の時間\(t\)における位置を表す式は、下記のようになります。
$$ \begin{align} \require{color} \textcolor{red} { cos (\omega t) } \textcolor{blue} { + j sin (\omega t) } &= \textcolor{red}{1} \textcolor{blue}{+ j \omega t} \textcolor{red} {- \displaystyle\frac{(\omega t)^2}{2!}} \textcolor{blue}{- j \displaystyle\frac{(\omega t)^3}{3!}} \textcolor{red}{+ \displaystyle\frac{(\omega t)^4}{4!}} \textcolor{blue}{+ j \displaystyle\frac{(\omega t)^5}{5!}} \textcolor{red} {- \displaystyle\frac{(\omega t)^6}{6!} } \cdots \\ &= \textcolor{red}{1} \textcolor{blue}{+ \displaystyle\frac{j \omega t}{1!}} \textcolor{red}{+\displaystyle\frac{(j \omega t)^2}{2!}} \textcolor{blue}{+\displaystyle\frac{(j \omega t)^3}{3!}} \textcolor{red}{+\displaystyle\frac{(j \omega t)^4}{4!}} \textcolor{blue}{+ \displaystyle\frac{(j \omega t)^5}{5!}} \textcolor{red}{+\displaystyle\frac{(j \omega t)^6}{6!}} \cdots \end{align}$$
これは、指数関数\( e^{j \omega t}\)をテイラー展開したものと等しくなるのです。
$$ e^{j \omega t} = 1+ \displaystyle\frac{j \omega t}{1!} +\displaystyle\frac{(j \omega t)^2}{2!} +\displaystyle\frac{(j \omega t)^3}{3!} +\displaystyle\frac{(j \omega t)^4}{4!} +\displaystyle\frac{(j \omega t)^5}{5!} +\displaystyle\frac{(j \omega t)^6}{6!} \cdots$$
したがって、正弦波を表す式は、複素数の形を用いれば、前記の式(13)のように表すことができるのです。
$$ \phi = e^{j \omega t} \tag{13} $$
速度ポテンシャル\( \phi\)を上記のように表すと、\(t\)で二階微分したものは\( – \omega ^2 e^{j \omega t} = – \omega ^2 \phi\)となります。 そうなると、一般式としての波動方程式(10)は、下記のように変形することができます。
$$ \begin{align} \displaystyle\frac{\partial ^2 \phi}{\partial t^2} &= c^2 \nabla ^2 \phi \\ – \omega ^2 \phi &= c^2 \nabla ^2 \phi \\ – \displaystyle\frac{\omega ^2}{c^2} \phi &= \nabla ^2 \phi \end{align}$$
ここで、\( k = \frac{ \omega}{c}\)であるため、上記式は下記のようにまとめることができます。
$$ – k \phi = \nabla ^2 \phi $$
$$ \unicode{x2234} \nabla ^2 \phi + k^2 \phi = 0 \tag{14}$$
そして、複素数として表した一般式としての波動方程式である式(14)を、式(12)と同じ要領で球面波における波動方程式として表すと、下記のようになります。
$$ \displaystyle\frac{\partial ^2 (r \phi)}{\partial r^2} + k^2 (r \phi) = 0 \tag{15} $$
点音源の速度ポテンシャルを求める
さて、ようやく波動方程式を解いて速度ポテンシャルを求める準備が整いました。
式(15)を今一度見てみますと、その形は、下記の微分方程式と同じ形をしていることがわかります。
$$ \displaystyle\frac{\partial^2 x}{\partial t^2} + \omega ^2 x = 0 $$
この微分方程式の一般解は下記の形となることが知られています。
$$ x = A e^{-j \omega t} + B e^{j \omega t} $$
上記一般解の形において、式(15)の解の形として表すと、下記のようになります。
$$ r \phi = A e^{-jkr} + B e^{jkr} \tag{16} $$
ここで、右辺の第一項は音源から外側に向かう音波を表し、第二項は外側から音源方向に向かう音波を表しています。音源方向に向かう音波というのは、例えば点音源と同じ位置の中心を持つ球形の壁に、点音源から放射された球面波が反射して戻ってくるような場合が考えられますが、スピーカーのように自由空間に音波を放射するような場合には意味のない項となります。
よって、( r \phi = A e^{-jkr})についてのみ検討します。まず、定数(A)を求めるために式(16)を変形すると、下記のようになります。
$$ \begin{align} r \phi &= A e^{-jkr} \\ \phi &= \displaystyle\frac{A}{r} e^{-jkr} \tag{17}\end{align} $$
これを\(r\)で微分すると下記になります。
$$ \begin{align} \displaystyle\frac{\partial \phi}{\partial r} &= \displaystyle\frac{\partial}{\partial r} \left( \displaystyle\frac{A}{r} e^{-jkr} \right) \\ &= \displaystyle\frac{A}{r^2} e^{-jkr} – jk \displaystyle\frac{A}{r} e^{-jkr} \\ &= \displaystyle\frac{A}{r^2} e^{-jkr} -jkr \displaystyle\frac{A}{r^2} e^{-jkr} \\ &= \displaystyle\frac{A}{r^2} (1-jkr) e^{-jkr} \end{align}$$
ここで、比較的近距離では\(kr\)<<1となり、\(-jkr\)→0となるため、上記式は、下記となります。
$$ \displaystyle\frac{\partial \phi}{\partial r} = \displaystyle\frac{A}{r^2}$$
速度ポテンシャル\( \phi\)を方向微分したものは、速度(この場合、空気の粒子速度\( V\))でしたので、\(A\)は下記となります。
$$ \begin{align} V &= \displaystyle\frac{A}{r^2} \\ \unicode{x2234} A &= V r^2 \end{align}$$
ところで、スピーカーは有限の面積の振動板が空気を動かすので、空気一粒の粒子速度ではなく、振動板面積の前方にある空気の体積が速度を持つと考え、体積速度を用いた形にします。球面波の場合の体積速度Qは、球の表面積\( 4 \pi r^2\)×粒子速度\( V\)で定義されます。そうすると、速度ポテンシャル\( \phi\)を求める式(17)は、下記のように変形することができます。
$$ \begin{align} \require{cancel} \phi &= \displaystyle\frac{A}{r} e^{-jkr} \\ &= \displaystyle\frac{V r^2}{r} e^{-jkr} \\ &= \displaystyle\frac{Q \cancel{r^2}}{4 \pi \cancel{r^2} r}e^{-jkr} \end{align} $$
さらに、時間因数\( e^{j \omega t}\)を含めますと、最終的に下記の式になります。
$$ \unicode{x2234} \phi = \displaystyle\frac{Q}{4 \pi r}e^{-j(kr- \omega t)} \tag{18}$$
この式(18)が、点音源の速度ポテンシャルを求める式となります。
次に、点音源における速度ポテンシャルから、無限大バッフルに取り付けた振動板が出力する音圧の式を求めます。