はじめに
仕事でスピーカーのエンクロージャの設計をするために、理論体系を勉強してEXCELで特性のシミュレータを作ったことがありました。ところが、仕事を変えてからというもの、久しぶりにEXCELに入力した式を見ても、「なんでこんな式入れてるんだっけなぁ」とかなり忘れてしまっているようです。
ということで、思い出しがてら、備忘録的にブログにアップしておこうと思います。もしかしたら誰かの役に立つかもしれないし。
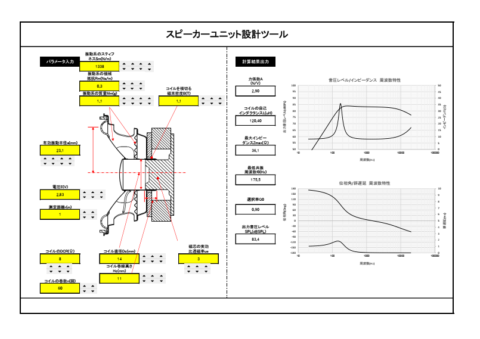
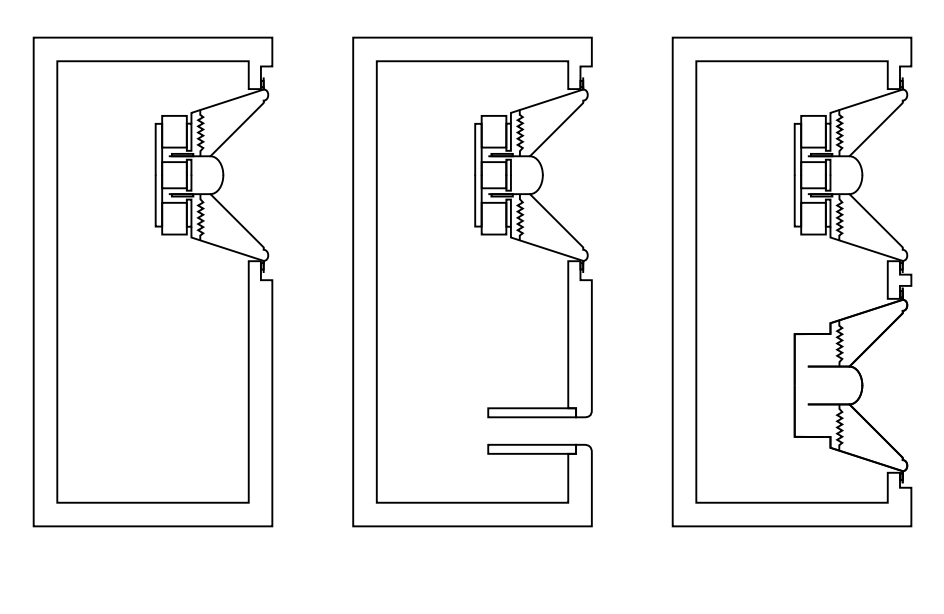
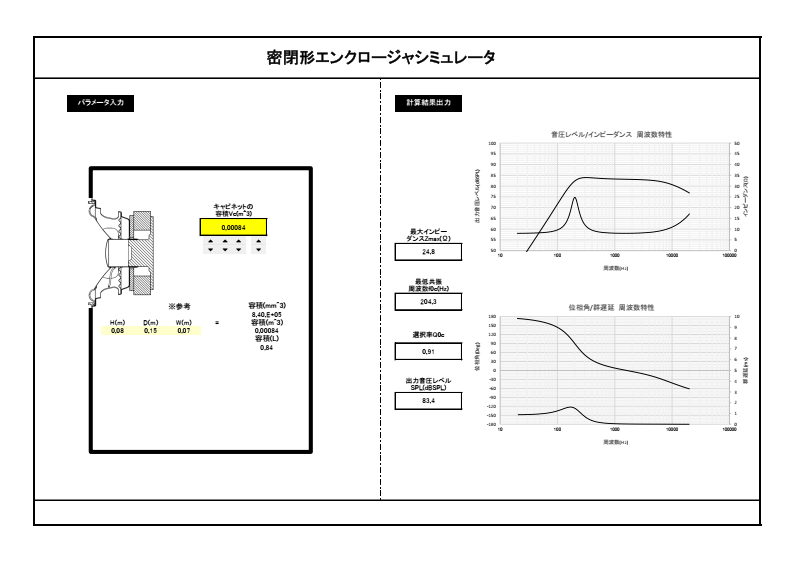
作ったシミュレータは、ドライバーユニット単品特性に加え、下図の3つのエンクロージャについてのシミュレータです。
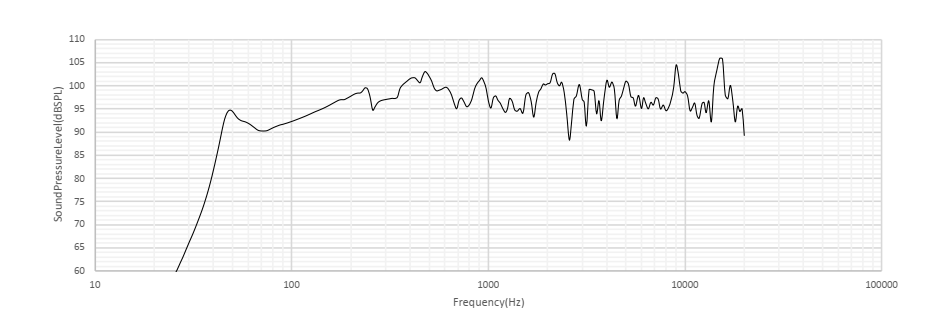
特性というのは周波数特性です。スピーカーの音質の評価にはしばしば周波数特性が用いられます。正確には出力音圧レベルの周波数特性を指しますが、周波数特性を見ることで大まかな音質の傾向をつかむことができます。
エンクロージャの設計方法に関しては、出力音圧レベルの周波数特性をシミュレーションするフリーソフトがいくつか公開されているようですが、音響理論に出てくる数式を使って、実際に計算してみるというところまでやってる実践的な解説記事や書籍は、意外に少ないような気がします。
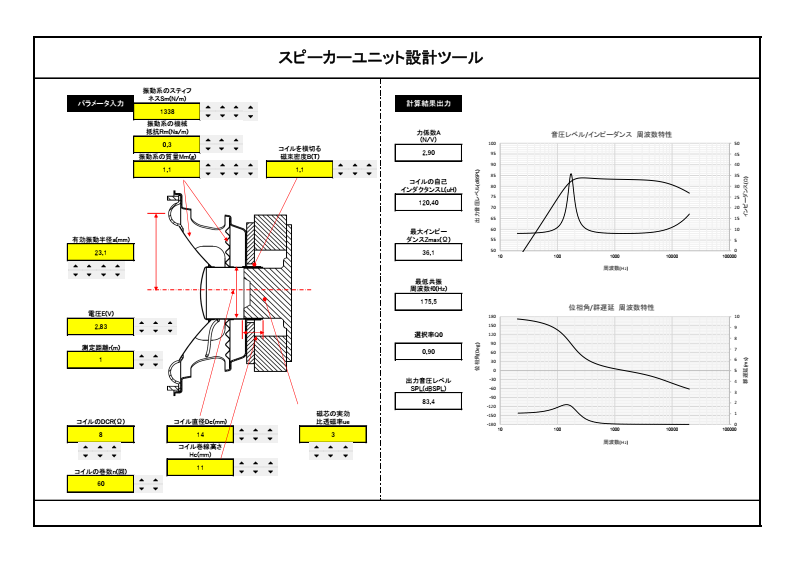
以前作成した周波数特性のシミュレータは、こんな感じのものです。
解説の流れ
EXCELデータはこちらからダウンロードできます。
著作権は弊社にありますが、自由に使用・配布・改良してください。ただし、有償で販売・貸与することはおやめください。主に学習用に作ってます。
なお、計算結果の利用については自己責任でお願いします。
それでは、下記の流れで解説していきます。
1.波動方程式を求める
2.速度ポテンシャルの導入
3.音圧の式を求める
4.インピーダンスの導入
5.粒子速度を求める
6.様々なエンクロージャの粒子速度を求める
7.EXCELでシミュレーションする
8.インピーダンス特性を求める
9.ダブルバスレフ型エンクロージャ
10.シミュレーションに使う定数の求め方
1~3は音圧を求めるための理論式の導出について書いてあります。
4~6は空気の粒子速度の求め方について書いてあります。
7はEXCELでの実際の作業について書いてあります。
8~10は番外編です。
理論式の式の導出は正直なところ参考文献の内容の書き直しですし、もっとわかりやすく解説してくださっている方もいらっしゃいますので、実務的には7だけ見てもらえればOKだと思います。
なお、スピーカーはボイスコイルが可動するダイナミック型であり、振動板がピストン運動できる周波数領域を対象としたシミュレーションとなっています。そのため、分割振動が生じる高音域では、実測値とシミュレーション値が大きく相違しますのでアテになりません。
スピーカーの出力音の音圧を表す式
音は空気が圧縮と膨張を繰り返しながら進む縦波の振動です。スピーカーの振動板が振動すると、目の前の空気を押したり引いたりすることで、大気圧に対して気圧が高くなったり低くなったりを繰り返します。その気圧の変化が波となって前方に進行することで音となります。このときの気圧の変動量が音圧です。
いきなりですが、スピーカーの出力音の周波数特性における音圧を表す式は、結論から書くと下記の式になります。
ここで、各符号は以下のとおりです。
\(p\):音圧(Pa)
\(\omega\):角速度(rad/s)
\(\rho_0\):空気の密度(kg/m \(^3\))
\(V\):振動している空気の粒子速度(m \(^3\)/s)
\(S_d\):振動板の面積(m \(^2\))
\(r\):振動板からの距離(m)
\(k=\omega/c\):波定数(1/m) ※\( c\):音速(m/s)
音圧を求める式がなぜこの式になるのか、先達方が導出してくださったことを説明してみたいと思います。
波動方程式を求める
音圧は波動方程式を解くことにより導出することができるようです。波動方程式というのは何やらカッコイイ名前の方程式ですが、波の動きを表す基本となる方程式です。波動方程式を用いることで、スピーカーの振動板から発生する音について、任意の位置における音圧を求めることができるようになります。
波動方程式は、連続の式と運動方程式から導出することができるということなので、まずはそれらの式について説明します。
連続の式
音は大気圧に対する気圧の変動です。しかし、風のように空気が前方に移動していくわけではありません。空気を小さな粒の集まりと考えたときに、粒ひとつひとつはその場で前後するように振動するだけであり、粒の疎の部分と密の部分とが、あたかも前方に移動していくように見えるのです。そのため、音波を疎密波と言ったりもします。
ここで、x方向・y方向・z方向の三次元の微小な空間を切り取って、その微小体積に粗密波が到達した場合を考えてみます。図で表すと、ちょうど下図のような感じです。この図では大きな立方体があるように見えますが、実際には相当ミクロな立方体を考えています。なので、\( (x,y,z) \)の位置も\( (x+Δx,y,z) \)の位置も、ほんの少しだけズレてるだけでほとんど同じくらいの位置であると考えてください。
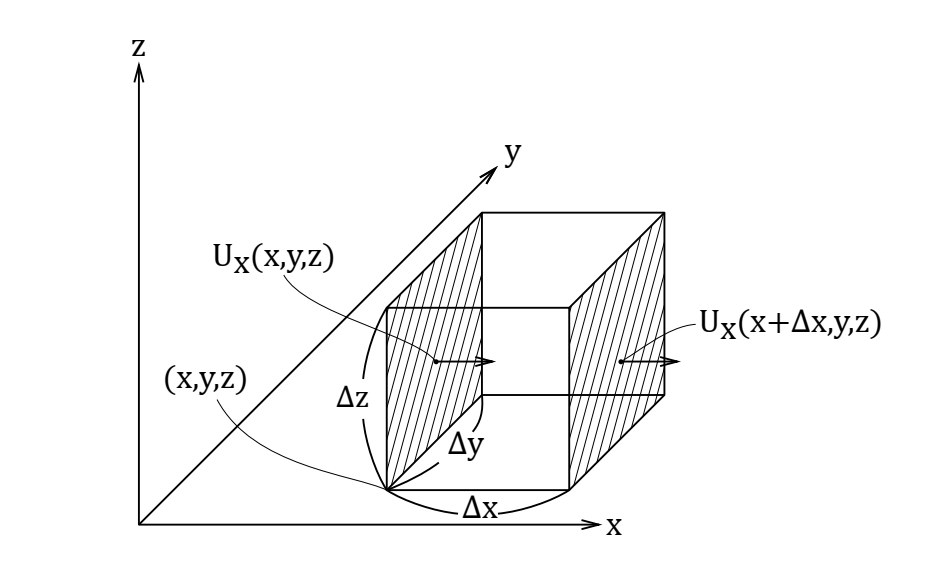
例えば、微小体積が密の状態になるということは、点\((x,y,z)\)に空気が一時的に流入したと考えられます。この点\((x,y,z)\)のx方向に流入する空気の質量(kg)は、大気の密度\(\rho_0\)×体積速度(m\(^3\)/s)×時間\(\Delta t\)で表すことができますので、x方向の速度を\(u_x(x,y,z)\)とすると、
$$\rho_0 u_x(x,y,z) \Delta y \Delta z \Delta t$$
と表現することができます。
また、微小体積のx方向の長さは\(\Delta x\)ですので、点\((x+\Delta x,y,z)\)のx方向に流入する空気の質量(kg)は、x方向の速度を\(u_x(x+ \Delta x,y,z)\)とすると、
$$ – \rho_0 u_x(x+ \Delta x,y,z) \Delta y \Delta z \Delta t $$
と表現することができます。
ここで、点\((x+ \Delta x,y,z)\)においては、実際には空気は流出するはずですので、流入量としてはマイナス方向となる点に注意が必要です。
さて、このように微小体積内に流入する空気の質量の収支は、x方向については
$$\rho_0 {u_x(x,y,z)-u_x(x+ \Delta x,y,z)} \Delta y \Delta z \Delta t$$
となります。
これをy方向とz方向についても足し合わせると、
$$\begin{align} \rho_0 [ &{u_x(x,y,z)-u_x(x+ \Delta x,y,z)} \Delta y \Delta z \\ + &{u_y(x,y,z)-u_x(x,y+ \Delta y,z)} \Delta x \Delta z \\ + &{u_z(x,y,z)-u_z(x,y,z+ \Delta z)} \Delta x \Delta y ] \Delta t \end{align} \tag{2}$$
となります。
一方、微小体積内の空気の密度に着目すると、時間の変動によって密度が変化しますので、微小体積内の空気の質量は下記のようにも表すことができます。
$$ { \rho(x,y,z,t+\Delta t)-\rho(x,y,z,t) } \Delta x \Delta y \Delta z $$
ここで、圧力変動\(p\)を受けて、単位質量当たりの体積\(v\)が\(\delta v\)だけ膨張した場合、\(p\)を圧縮率\(- \frac{\delta v}{v}\)で割ったものを体積弾性率\(\kappa\)といいます。密度\(\rho\)は比体積である\(v\)の逆数ですので、圧縮率\(-\frac{\delta v}{v}\)は、大気の密度を\(\rho_0\)、微小体積内の増加した密度を\(\rho\)としたときに、\(\frac{\rho}{\rho_0}\)と表現しても等価となります。したがって、上記式は、体積弾性率\(\kappa\)を用いて下記の式に変形することができます。
$$ \dfrac{\rho_0}{\kappa} { p(x,y,z,t+\Delta t)-p(x,y,z,t) } \Delta x \Delta y \Delta z \tag{3} $$
上記の式(2)と(3)は、いずれも微小体積内に空気が流入した際の空気の質量を表しているため、(2)と(3)は等しくなるはずですので、下記の等式が成り立ちます。
$$ \require{cancel} \begin{align} \cancel{\rho_0} [ &{u_x(x,y,z)-u_x(x+ \Delta x,y,z)} \Delta y \Delta z \\ + &{u_y(x,y,z)-u_x(x,y+ \Delta y,z)} \Delta x \Delta z \\ + &{u_z(x,y,z)-u_z(x,y,z+ \Delta z)} \Delta x \Delta y ] \Delta t \\ &= \displaystyle\frac{\cancel{\rho_0}}{\kappa} { p(x,y,z,t+\Delta t)-p(x,y,z,t) } \Delta x \Delta y \Delta z \end{align} $$
この両辺に\(\kappa\)を乗じ、\(\Delta x \Delta y \Delta z \Delta t\)で割ると、
$$ \begin{align} \displaystyle\frac{p(x,y,z,t+\Delta t)-p(x,y,z,t)}{\Delta t} &= -\kappa \left( \dfrac{u_x(x+\Delta x,y,z,t)-u_x(x,y,z,t)}{\Delta x} \\ +\displaystyle\frac{u_y(x,y+\Delta y,z,t)-u_y(x,y,z,t)}{\Delta y} \\ +\displaystyle\frac{u_z(x,y,z+\Delta z,t)-u_z(x,y,z,t)}{\Delta z} \right) \end{align} $$
となります。
さて、これまでの検討では、微小体積として一定の体積を有する空間について検討してきましたが、理論としては体積が限りなくゼロであり、時間も限りなくゼロにおける状況としなければ正確な式になりません。そこで、\( \Delta x \)・\( \Delta y \)・\( \Delta z \)・\( \Delta t \)→0の極限をとります。すると、式(3)は下記となります。
$$ \displaystyle\frac{\partial p}{\partial t}=- \kappa \left( \displaystyle\frac{\partial u_x}{\partial x}+\displaystyle\frac{\partial u_y}{\partial y}+\displaystyle\frac{\partial u_z}{\partial z} \right) \tag{4} $$
この式(4)を連続の式と呼びます。
運動方程式
連続の式の説明で用いた微小体積内について、次は空気の運動の観点から検討します。
まずx方向について検討してみます。再び微小体積の図を示しますが、今回は微小体積のYZ面に外力\(F\)が作用すると考えます。ただし、実際にはYZ面全体に一様な圧力\(p\)が作用する形となります。
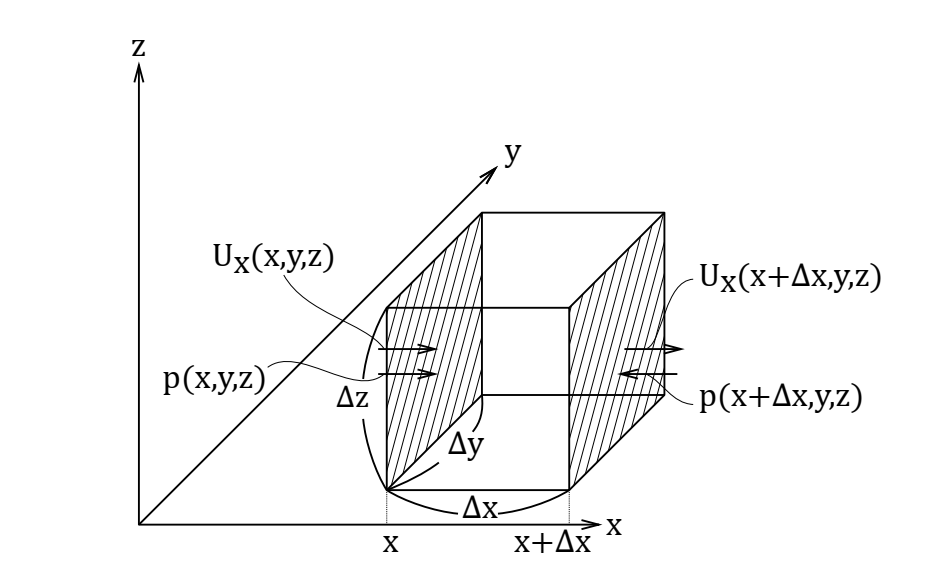
物質の運動を表す方程式として、ニュートンの運動方程式\( F=ma \)を適用してみますと、加速度\( a \)はx方向の速度\( u_x \)を\( t \)で微分したもの(傾きを求めたもの)ですので、
$$ F=ma=\rho_0 \Delta x \Delta y \Delta z \displaystyle\frac{\partial u_x}{\partial t} $$
となります。
また、外力\( F \)は、微小面積\( \Delta y \Delta z \)に圧力差を乗ずることにより求めることができ、
$$ { p(x+\Delta x,y,z,t)-p(x,y,z,t) } \Delta y \Delta z $$
となります。よって、x方向の運動方程式は下記となります。
$$ \require{cancel} { p(x+\Delta x,y,z,t)-p(x,y,z,t) } \cancel{\Delta y \Delta z}= \rho_0 \Delta x \cancel{\Delta y \Delta z} \displaystyle\frac{\partial u_x}{\partial t}$$
$$ \unicode{x2234} \displaystyle\frac{\partial u_x}{\partial t}= – \displaystyle\frac{1}{\rho_0} \displaystyle\frac{p(x+\Delta x,y,z,t)-p(x,y,z,t)}{\Delta x} $$
ここで、理論的に正確な式とするために\( \Delta t \)→0の極限を考えます。また、x方向と同様にy方向及びz方向の運動方程式についても考えてみると、下記の式にまとめることができます。
$$ \begin{align} \displaystyle\frac{\partial u_x}{\partial t}&=-\displaystyle\frac{1}{\rho_0} \displaystyle\frac{\partial p}{\Delta x} \\ \displaystyle\frac{\partial u_y}{\partial t}&=-\displaystyle\frac{1}{\rho_0} \displaystyle\frac{\partial p}{\Delta y} \\ \displaystyle\frac{\partial u_z}{\partial t}&=-\displaystyle\frac{1}{\rho_0} \displaystyle\frac{\partial p}{\Delta z} \end{align} \tag{5} $$
波動方程式
さて、いよいよ波動方程式を導出します。まず、準備段階として、連続の式(4)は両辺を\( t \)で微分し、運動方程式(5)は両辺をそれぞれ\( x,y,z \)で微分します。突然なぜ微分するのかと疑問に思いますが、微分することで二つの式に共通項が生まれるようになり、共通項を代入することで一つの式にすることができるのです。なお、両辺を微分するので、方程式の等号の関係は崩れません。
連続の式の両辺を\( t \)で微分すると、
$$ \displaystyle\frac{\partial}{\partial t} \left( \displaystyle\frac{ \partial p}{\partial t} \right) = \displaystyle\frac{\partial}{\partial t} \displaystyle\left\{ – \kappa \left( \dfrac{\partial u_x}{\partial x} + \displaystyle\frac{\partial u_y}{\partial y} + \displaystyle\frac{\partial u_z}{\partial z} \right) \displaystyle\right\} $$
となります。
これを整理すると下記の式が得られます。
$$ \dfrac{\partial ^2}{\partial t^2} = – \kappa \left( \dfrac{\partial ^2 u_x}{\partial x \partial t} + \dfrac{\partial ^2 u_y}{\partial y \partial t} + \dfrac{\partial ^2 u_z}{\partial z \partial t} \right) \tag{6} $$
次に、運動方程式のそれぞれの式の両辺を\( x,y,z \)で微分すると、
$$ \begin{align} \displaystyle\frac{\partial ^2 u_x}{\partial x \partial t} &= – \displaystyle\frac{1}{\rho_0} \dfrac{\partial^2 p}{\partial x^2} \\ \displaystyle\frac{\partial ^2 u_y}{\partial y \partial t} &= – \displaystyle\frac{1}{\rho_0} \displaystyle\frac{\partial^2 p}{\partial y^2} \\ \displaystyle\frac{\partial ^2 u_z}{\partial z\partial t} &=- \displaystyle\frac{1}{\rho_0} \displaystyle\frac{\partial^2 p}{\partial z^2} \end{align} \tag{7} $$
となります。
これで準備が整いましたので、運動方程式(7)を連続の式(6)に代入します。
$$ \displaystyle\frac{\partial ^2 p}{\partial t^2}=\displaystyle\frac{\kappa}{\rho_0} \left( \displaystyle\frac{\partial ^2 p}{\partial x^2}+\displaystyle\frac{\partial ^2 p}{\partial y^2}+\displaystyle\frac{\partial ^2 p}{\partial y^2} \right) \tag{8} $$
ここで、二階の偏微分の部分を\(\nabla^2\)としてまとめます。この\(\nabla^2\)をラプラシアンと呼びます。また、\(\sqrt{\frac{\kappa}{\rho_0}}\)は音速\(c\)として表すことができます。そうなると、下記の式のようにすっきりした形となります。
$$ \displaystyle\frac{\partial ^2 p}{\partial x^2} = c^2 \nabla ^2 p \tag{9} $$
これを音響伝搬に関する波動方程式と呼びます。